本文摘自:
https://www.ast.gg/卷积优化#8326b45e68f14e958ac44170e609013e
GEMM优化
基于算法分析的方法
Strassen 算法
Coppersmith–Winograd 算法
为什么不用呢?
通过展开循环,尽量减少访存指令占比
naive version:
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n++) {
C[m][n] = 0;
for (int k = 0; k < K; k++) {
C[m][n] += A[m][k] * B[k][n];
}
}
}访存数: 4MNK, 但编译器可能优化到2MNK?
version1:
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n += 4) {
C[m][n + 0] = 0;
C[m][n + 1] = 0;
C[m][n + 2] = 0;
C[m][n + 3] = 0;
for (int k = 0; k < K; k++) {
C[m][n + 0] += A[m][k] * B[k][n + 0];
C[m][n + 1] += A[m][k] * B[k][n + 1];
C[m][n + 2] += A[m][k] * B[k][n + 2];
C[m][n + 3] += A[m][k] * B[k][n + 3];
}
}
}访存数:(8+1+4)/4 MNK = 13/4 MNK(寄存器数量够的话,编译器可能优化到5/4 MNK?)
version2:
for (int m = 0; m < M; m += 4) {
for (int n = 0; n < N; n += 4) {
C[m + 0][n + 0..3] = 0;
C[m + 1][n + 0..3] = 0;
C[m + 2][n + 0..3] = 0;
C[m + 3][n + 0..3] = 0;
for (int k = 0; k < K; k++) {
C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];
C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];
C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];
C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];
}
}
}访存数:(16*2 + 4 + 4) / 16MNK = 5/2 MMN, 编译器优化后可达:1/2MNK
version3:
for (int m = 0; m < M; m += 4) {
for (int n = 0; n < N; n += 4) {
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
C[m + 0..3][n + 0..3] = 0;
for (int k = 0; k < K; k += 4) {
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];
C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];
}
}
}访存数:(16*2 + 16 + 16) / 64MNK = 1 MNK, 编译器优化后可达:1/2MNK
如果存在编译器优化的情况下,这一维度的展开还会带来perf 提升吗?
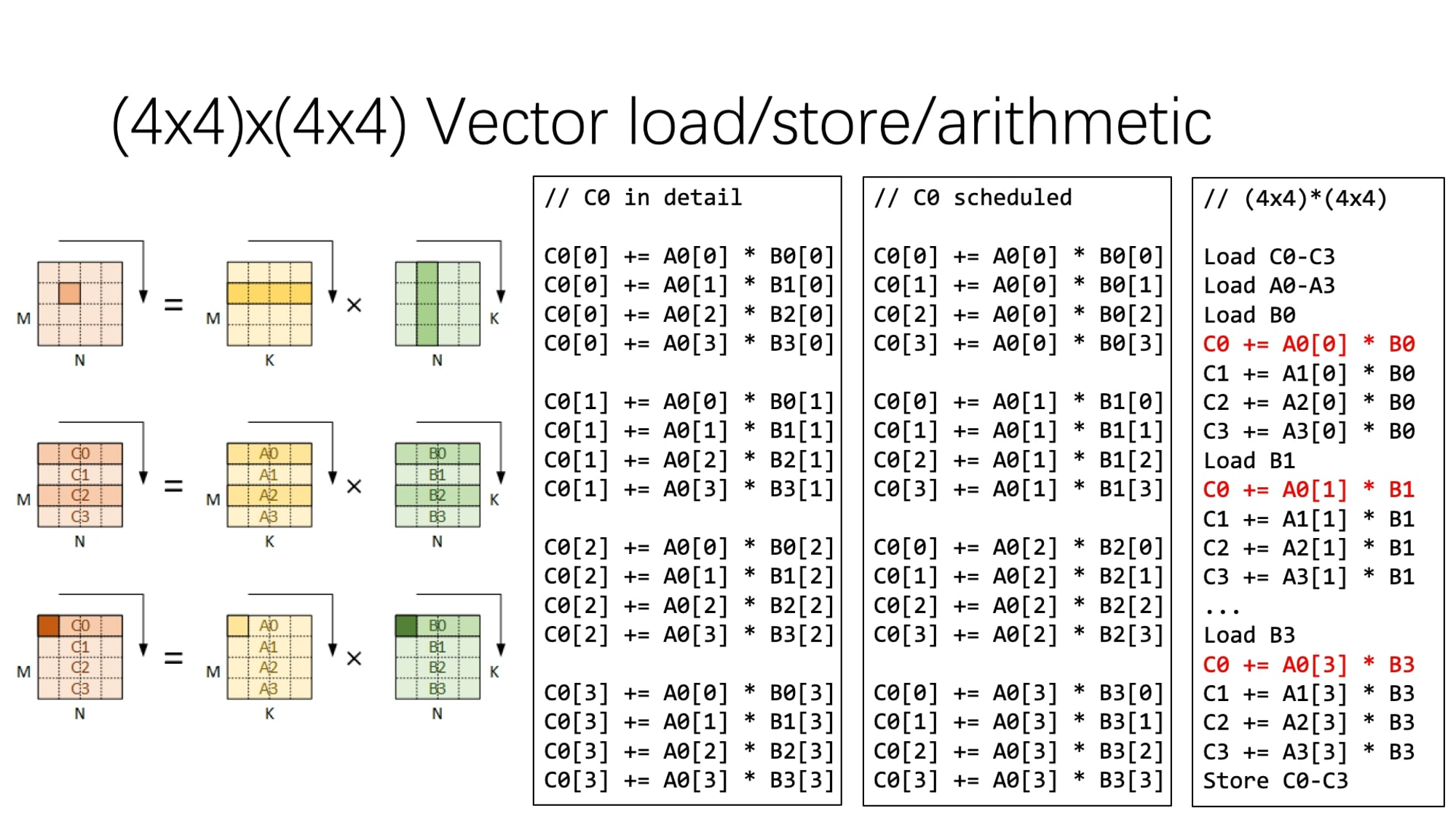
对于支持SIMD的平台,进行向量化的支持
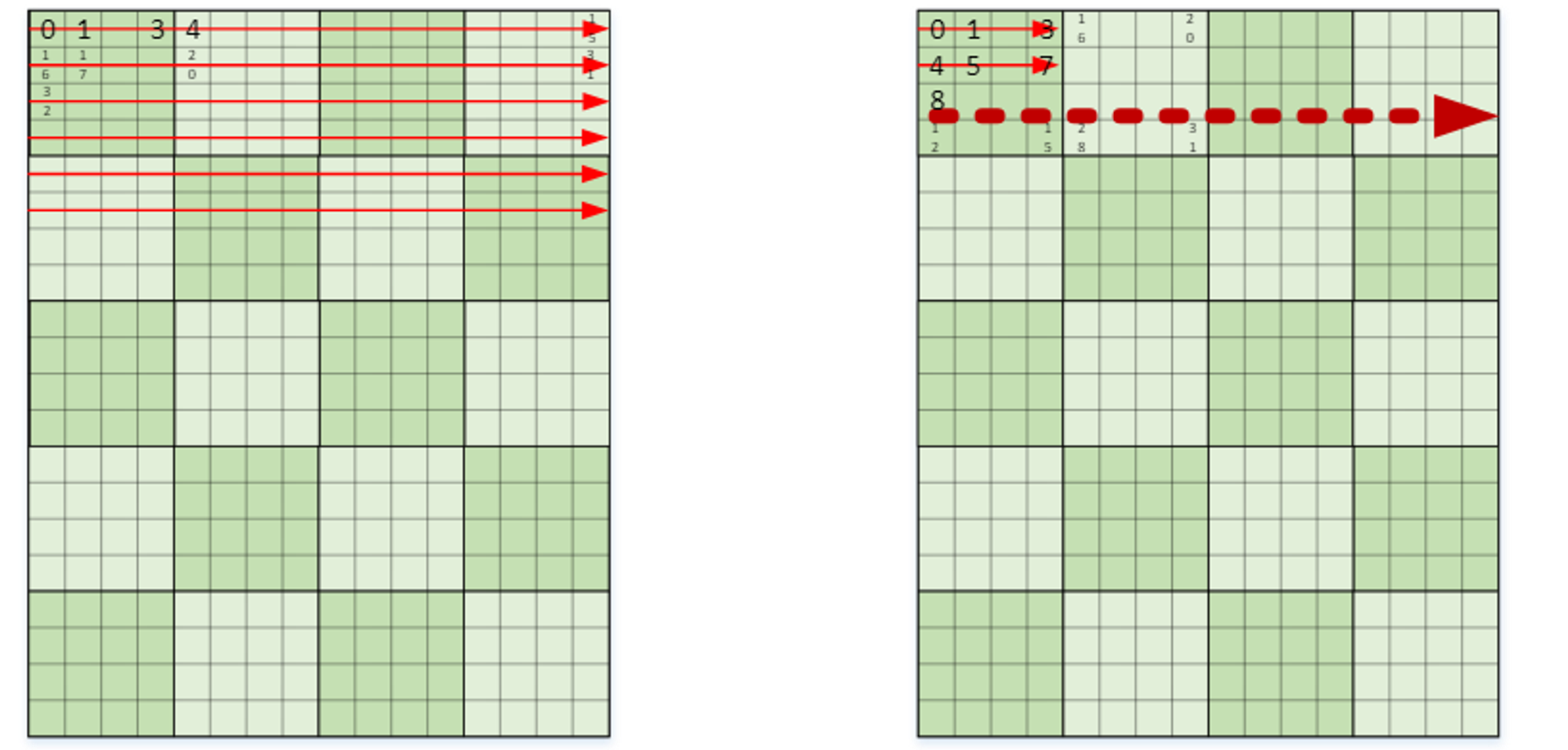
优化内存布局,减少cache miss
使用图中右边的内存布局,减少一个块内的cache miss以及块间的cache miss
QNNPACK
卷积(Conv)优化
im2col

内存布局的影响
NCHW:
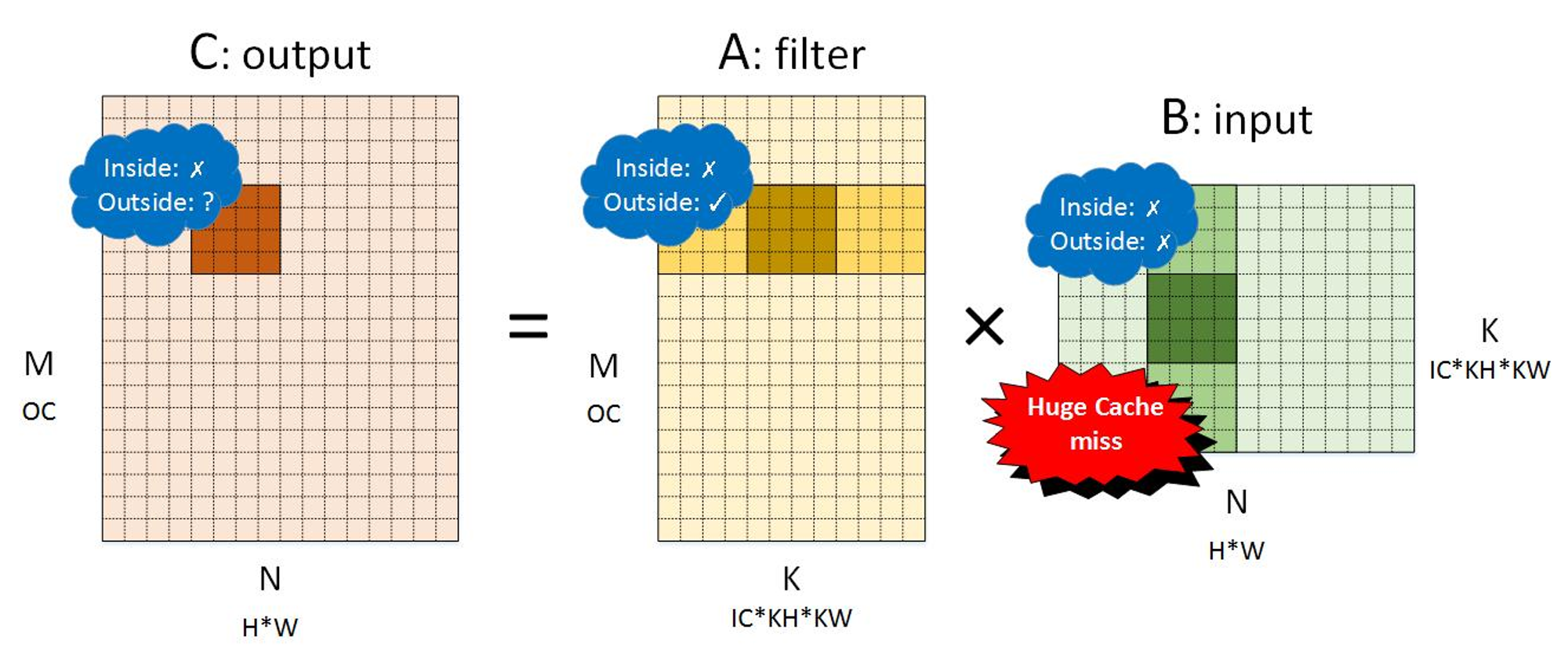
NHWC:
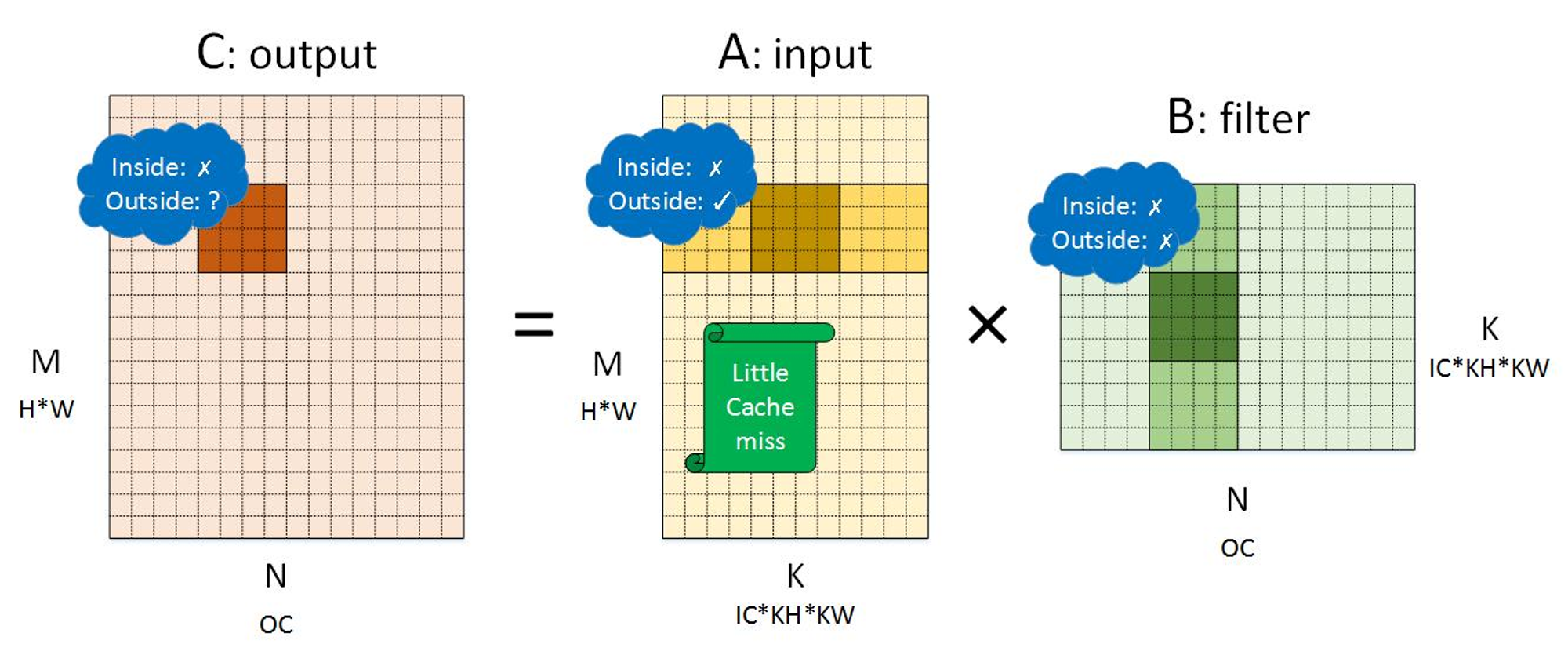
输出:两种布局都一样,因为输出没有访存复用
输入:NHWC优于NCHW,因为前者在小块间的局部性更高
filter:NCHW优于NHWC,因为前者在小块间的局部性更高。但是通常filter可以在模型准备阶段转换内存布局,因为一般filter的内容是固定的
空间组合优化算法
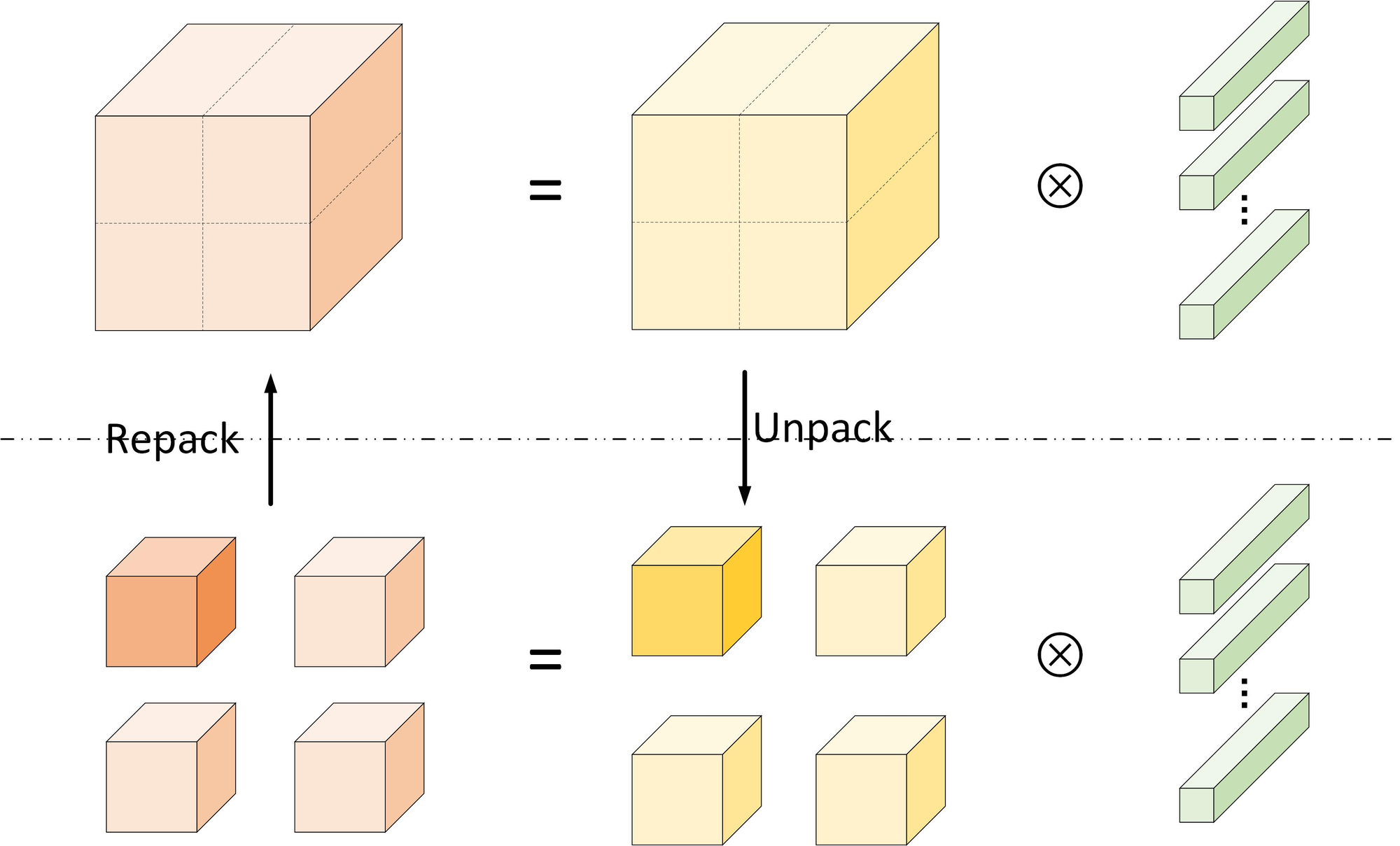
将大输入的tensor划分成小的tensor,卷积后的得到部分输出tensor,再组合起来。划分的目的是为了增加局部性。同时由于卷积计算的特点,以及padding的存在,划分粒度越细,额外的内存开销就越大。
当划分粒度最细时,退化到成im2col。
最优的划分粒度对于不同规模的卷积,不同的架构平台可能都是不同的 ,该粒度的寻找可以通过自动化的方式完成:autoTvm.
Winograd算法
1D

2D
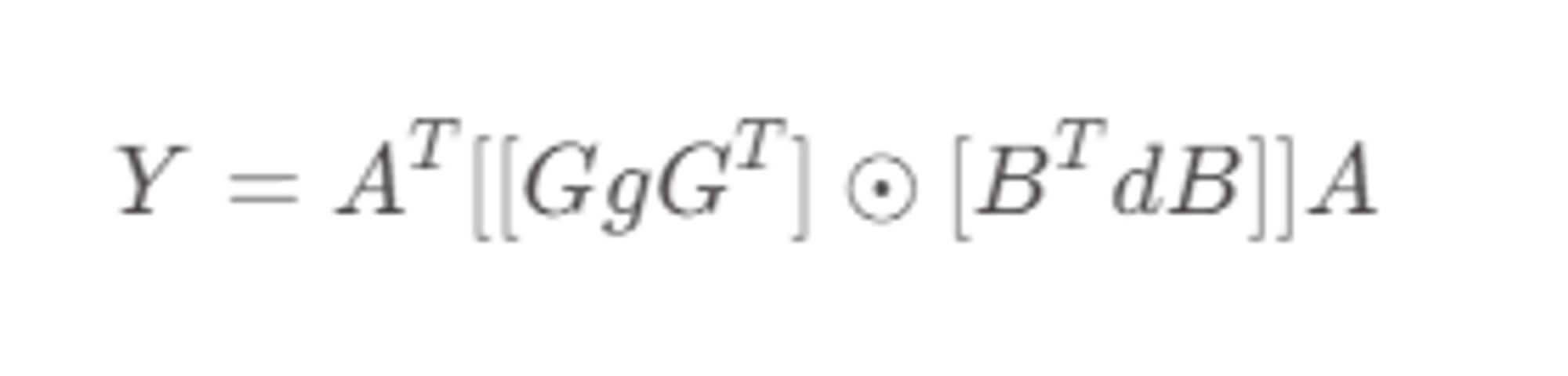
工程实现
间接卷积优化算法
im2col的过程需要额外的内存空间开销,以及数据拷贝的时间开销。而间接卷积优化算法则使用一种间接寻址的方法避免了这两个问题。
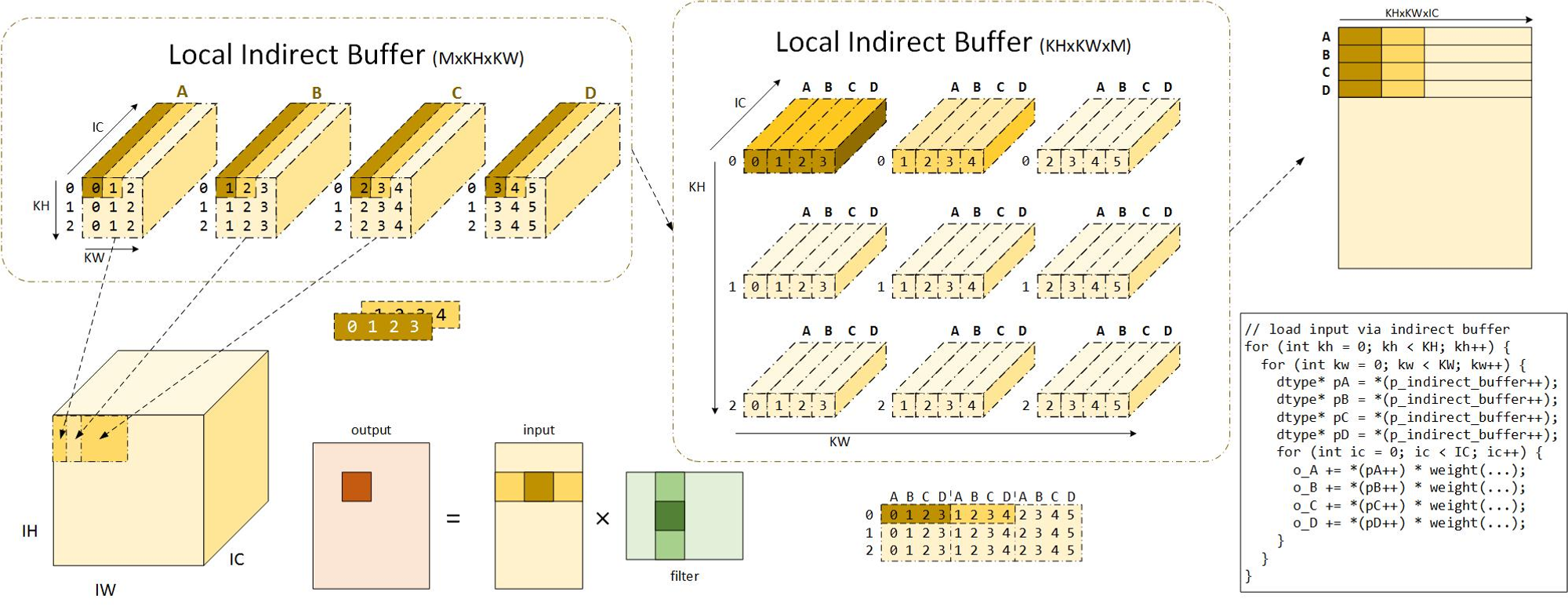
并且也可以巧妙的解决pading带来的拷贝问题。
problem:
这种方法的cache友好度如何?
通过使一次计算M*N所需要的输入数据重排为连续的来提升cache友好度?



评论